People’s choices determine a partial ordering over people’s desirability

Consider the following relationship:

$$ \delta_{i}(a, b) = \begin{cases} -1 \text{ if person i has chosen person b over person a} \\ 0 \text{ if person i has not made a choice between person a and person b} \\ 1 \text{ if person i has chosen person a over person b} \end{cases} $$ $$ a \le b \text{ iff } \sum_{i} \delta_{i}(a, b) < 0$$

Is this a partial ordering?

For a relationship to be a partial ordering, it has to be the case that:

$$ a \le a \text{ (Reflexivity)} $$ $$ (a \le b) \land (b \le a) \implies a = b \text{ (Antisymmetry)}$$ $$ (a \le b) \land (b \le c) \implies a \le c \text{ (Transitivity)}$$

Antisymmetry

We do get antisymmetry, since it can’t be the case that both of these are true at the same time:

$$ \sum_{i=0}^n \delta_i(a, b) < 0 $$ $$ \sum_{i=0}^n \delta_i(b, a) = - \sum_{i=0}^n \delta_i(a, b) < 0 $$

Reflexivity

We can also get reflexivity, by dictating that $ a \le a $.

Transitivity

We don’t get transitivity for free, because you could have a rock-papers-scissors situation. For example, consider a situation where you have a, an attractive celebrity, b, the less attractive but still pretty cool friend of that celebrity, and c, the husband of a’s childhood sweetheart. Then:

$ b \le a $, because of the people who choose between a and b, they mostly choose a
$ c \le b $, because of the people who choose between b and c, they mostly choose b
$ a \le c $, because the only person who chooses between a and c is c’s wife, who chooses c

And if fact you do see this kind of thing in some animals.

With regard to their throat color, the males of the common side-blotched lizard can also be distinguished into three morphotypes which compete against each other for reproduction. Males with an orange-colored throat aggressively claim a large territory for themselves to build a harem. Meanwhile, the males with a blue-colored throat are less dominant, but guard their mating partner from other males. Finally, males with a yellow-colored throat mimic the female phenotype and rely on a sneaking strategy. From that polymorphism, a rock-paper-scissor like game emerges: the dominant orange-colored males take females from the blue-colored males by force, the blue-colored males are able to protect their females from the yellow-colored males, which in turn are able to sneak into the harem of orange-colored males. –Wikipedia, Alternative mating strategy: Common side-blotched lizard

Even worse, you might still have a situation where

70% of people are indifferent between a and b, and 30% prefer a
70% of people are indifferent between b and c, and 30% prefer b
70% of people are indifferent between c and a, and 30% prefer c

Attaining transitivity

However, we might have the intuition that these types of loops are rare. And so we can define a second relationship:

$$\begin{eqnarray} a \le_2 b \text{ iff } \nonumber \\ &\text{ there exists some chain such that } a \le x_1 \le ... \le x_n \le b \text{, possibly just } a \le b \tag{1} \\ &\text{ AND there is no chain such that } b \le x_1 \le ... \le x_n \le a \tag{2} \\ &\text{ AND there is no chain such that } c \le y_1 \le ... \le y_l \le a \le x_1 \le ... \le x_m \le b \le z_1 \le ... \le z_n \le c \tag{3}\\ \end{eqnarray}$$

So basically, we synthetically force transitivity, but we remove the places where there are loops, to preserve antisymmetry.

Now, if $a \le_2 b$ and $b \le_2 c $, then $ a \le_2 c $, because we can concatenate the chains from (1), and staring at the other two properties should also convince the reader that they are fulfilled.

How does this look?

So now we have a partial ordering. There is no absolute highest or lowest point, but there is some notion of higher and lower:

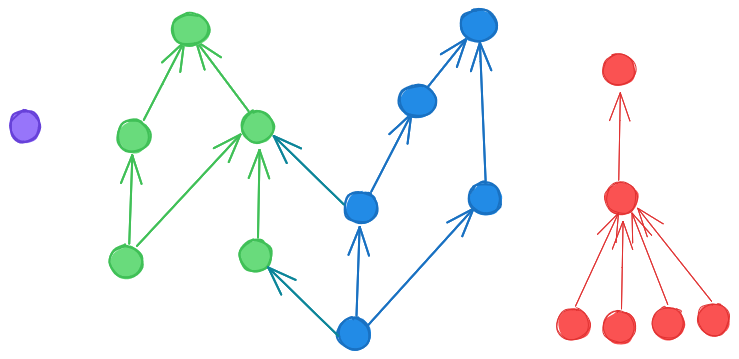
Blue and green might be two partially overlapping social groups, red a separate clique, and purple someone who married their childhood sweetheart.

But why think about this?

I think grounding thoughts on people’s choices has the potential to cut through a bunch of bullshit and platitudes. Personally, I am interested in occasionally using these concepts to make inferences about what people’s future chances and choices are. For example, I want to be able to notice that past romantic success is correlated with future romantic success, or to notice that some actions result in sliding down the graph induced by people’s choices, or pay some attention to what characteristics correlate with being up in the graph. For me, the graph adds clarity.